Die Impulse sind bereits in rechter Abbildung eingetragen. Innere Linien gibt es nicht. Zum Vertex gehört der Faktor g ~ 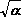 .
Für ihn wird daher
-ig
notiert.
.
Für ihn wird daher
-ig
notiert.
Da es keine internen Linien gibt, enthält M auch keinen Beitrag durch Propagatoren. Die Deltafunktion für den einzigen Vertex lautet: Da es keinen internen Impulse gibt, entfällt die Integration darüber. Die eben eingesetzte Deltafunktion wird wieder gestrichen. Es bleibt lediglich der Ausdruck -ig übrig, der gleich -i M gesetzt wird. Aus -i M = -ig folgt natürlich sofort: M = g Die Amplitude (in niedrigster Ordnung) ist also gleich der Wurzel aus der Kopplungskonstanten (g ~ 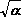 ).
).
Mit dieser Amplitude können wir die Zerfallsrate des Prozesses berechnen um sie dann z.B. experimentell zu überprüfen.
|
|||||||||

