|
Streu-Experimente
-
Der differenzielle Wirkungsquerschnitt (Interpretation)
|
Wir haben bisher herausgefunden,
das
s Teilchen, die durch das Flächenelement
d
s
fliegen, in das entsprechende
|
Raumwinkelelement d
W
gestreut werden.
|
|
 Gibt
es einen Zusammenhang zwischen d
s
und
d
W
?
Gibt
es einen Zusammenhang zwischen d
s
und
d
W
?
Ja! Je größer wir
d
s
machen, desto größer wird auch d
W
.
Der
Quotient D
aus d
s
und d
W
und ist eine Größe, die im einfachsten Fall nur vom Streuwinkel
q
und dem Stoßparameter
b abhängt. Da man b durch
q
ausdrücken kann (und
umgekehrt), hängt D im Prinzip nur von
|
q
(bzw. nur von b) ab. Es gilt also D = D(
q
) (bzw. D = D(b)). Der Quotient lautet dementsprechend:
 D(
q
)
= d
s/
d
W
D(
q
)
= d
s/
d
W
Man bezeichnet den Quotienten aus "Eintrittsflächen- und Raumwinkelelement" d
s
/
d
W
als differenziellen Wirkungsquerschnitt.
|
|
 Was
kann man sich darunter vorstellen? Wie wird d
s
/
d
W
gemessen?
Was
kann man sich darunter vorstellen? Wie wird d
s
/
d
W
gemessen?
Dazu muss man zuerst etwas über Teilchendetektoren (d.h. Teilchen- "Zähler") wissen. Kugel- oder zylinderförmig um ein Target herum angeordnet, manchmal auch als Wand dahinter, befinden sich viele einzelne Teilchendetektoren. Solche
Anordnungen nennt man
Detektor-Arrays (engl. "array", bedeutet "Aufstellung"). Jeder einzelne Detektor zählt die Teilchen, die durch seine Eintrittsfläche
A
D
treten (siehe die Skizze rechts, dort sind zwei Detektoren als blaue Quader angedeutet). Bei Messungen treten alle Teilchen, die in das Raumwinkelelement
d
W
gestreut werden in die Eintrittsfläche
A
D
eines einzelnen Detektors ein, der auch die Energie der einfallenden Teilchen messen kann. Da es sich hier nicht mehr um ein infinitesimal kleines, sondern
um ein
|

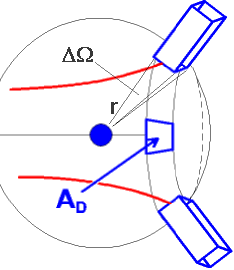 |
makroskopisches Raumwinkelelement handelt, schreiben wir
nicht mehr d
W
sondern
DW
. Das Bild rechts zeigt ein Detektor-Array des Hermes-Detektors bei DESY. Ein Physiker schließt gerade Datenleitungen an einzelne Detektoren an.
Für
eine Messung ist
DW
also eine feste bekannte Größe (
DW
= A
D
/r
2
).
|
|
|
Jeder
einzelne Detektor misst eine Teilchenrate dN
Detektor
/dt
(Anzahl einfallender Teilchen pro Zeiteinheit). dN
Detektor
/dt
ist proportional zum differenziellen Wirkungsquerschnitt
|
d
s
/
d
W
. Der Proportionalitätsfaktor kann durch Gleichung (1) beschrieben werden.
Es
gilt also:
|
|

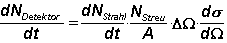 (1)
(1)
 N
Streu
/A bezeichnet dabei die Flächendichte der Streuzentren. Sie ist eine Materialkonstante.
N
Streu
/A bezeichnet dabei die Flächendichte der Streuzentren. Sie ist eine Materialkonstante.
 DW
ist
die das bekannte
Raumwinkel
element
DW
ist
die das bekannte
Raumwinkel
element
 dN
Strahl
/dt
ist die
Strahlteilchenrate
liefert jeder einzelne Detektor für sein
Raumwinkel
element
dN
Strahl
/dt
ist die
Strahlteilchenrate
liefert jeder einzelne Detektor für sein
Raumwinkel
element
 dN
Detektor
/dt
liefert jeder einzelne Detektor für sein Raumwinkelelement
dN
Detektor
/dt
liefert jeder einzelne Detektor für sein Raumwinkelelement
Man kann folglich aus dieser Messung den differenziellen Wirkungsquerschnitt
für
jeden Streuwinkel berechnen. Die Messgenauigkeit des Streuwinkels ist dabei durch die Größe der Eintrittsfläche in den einzelnen
Detektor bestimmt. Um es noch einmal deutlich zu machen:
Für
jeden
einzelnen Detektor bzw. den
|
damit verbundenen Streuwinkel
q
wird ein Wert
d
s/
d
W
bestimmt.
Der Genauigkeit halber muss man daher
d
s(q)/
d
W
schreiben, um die Abhängigkeit des differenziellen Wirkungsquerschnitts vom Streuwinkel
zu verdeutlichen.
|
|
Löst
man Gleichung (1) nach
d
s/
d
W
auf, erhält man:
 Unter
der Voraussetzung, dass
dt ein messbar kleines Zeitintervall und
dann
dN
Detektor
und
dN
Strahl
messbare
ganze Zahlen sind, kann man wiederum vereinfachen zu:
Unter
der Voraussetzung, dass
dt ein messbar kleines Zeitintervall und
dann
dN
Detektor
und
dN
Strahl
messbare
ganze Zahlen sind, kann man wiederum vereinfachen zu:

|
N
Detektor
/N
Strahl
ist nichts anderes als das Verhältnis aus der "Anzahl der Teilchen, die in einen bestimmten einzelnen Detektor gestreut wurden, geteilt durch die Anzahl
der Teilchen, die insgesamt im Strahl waren".
Somit ist
N
Detektor
/N
Strahl
nichts anderes als die Wahrscheinlichkeit für ein Teilchen des Strahls in das Raumwinkelelement des Detektors gestreut zu werden. Daraus folgt
dann endlich:
 Der differenzielle Wirkungsquerschnitt ist proportional zur Wahrscheinlichkeit dafür,
dass ein Teilchen in ein bestimmtes Raumwinkelelement gestreut wird.
Der differenzielle Wirkungsquerschnitt ist proportional zur Wahrscheinlichkeit dafür,
dass ein Teilchen in ein bestimmtes Raumwinkelelement gestreut wird.
|
|
|
Ergibt
die Auswertung einer Messung, dass für den Streuwinkel
q
1
der differenzielle Wirkungsquerschnitt
d
s
(
q
1
)/
d
W
doppelt so groß ist wie für einen anderen Streuwinkel
q
2, so bedeutet das, dass die Wahrscheinlichkeit pro Raumwinkel für ein
Teilchen, unter dem Winkel
q
1
|
gestreut zu werden
doppelt
so groß ist, wie unter
q
2
. Für eine gegebene Versuchsanordnung würde man folglich erwarten,
dass der Detektor, der unter dem Winkel
q
1
getroffen wird, doppelt so viele Teilchen registriert wie der Detektor
unter dem Winkel
q
2
.
|
|
|