|
Streu-Experimente -
Der differenzielle Wirkungsquerschnitt
 Wohin wird ein Teilchen an einem Streuzentrum gestreut, wenn man seinen
Stoßparameter
b um db vergrößert?
Wohin wird ein Teilchen an einem Streuzentrum gestreut, wenn man seinen
Stoßparameter
b um db vergrößert?
Beispiel:
Wir verwenden wieder unser Beispiel der Coulomb-Streuung von Elektronen an einem negativ geladenen Streuzentrum. Betrachte dazu folgende Abbildung.
|
Zuerst wird ein Teilchen mit Stoßparameter b (
rote
Bahn) gestreut, dann das gleiche Teilchen mit Stoßparameter b + db (
grüne
Bahn).
|
|
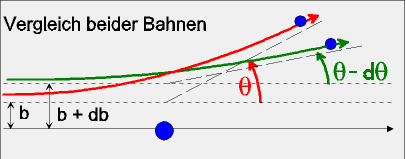
 Man erkennt, dass eine Vergrößerung des Stoßparameters um db zu einer Streuwinkelverkleinerung d
q
führt.
Man erkennt, dass eine Vergrößerung des Stoßparameters um db zu einer Streuwinkelverkleinerung d
q
führt.
|
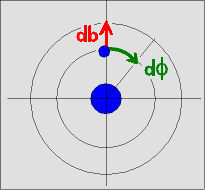
Betrachten wir nun die Situation in Flugrichtung. Neben einer Vergrößerung
db
des Stoßparameters könnte man die Bahn des Elektrons auch so ändern, dass es an der Stelle durch die Zielscheibe fliegt, die durch eine Drehung um den Winkel
d
f
aus der ursprünglichen Stelle hervorgeht (in Abbildung rechts als Drehung um
d
f
nach rechts dargestellt).
|
 |
|
Fasst man alle Kombinationen der beiden Änderungen
db
und
d
f
(oder kleinere) zusammen, kann man auch eine kleine Fläche
d
s
als mögliche Menge aller Änderungen betrachten (siehe Abbildung links; Blick in Flugrichtung!).
d
s
stellt
|
eine kleine Änderung des Wirkungsquerschnitts dar. Die Länge des kleinen Kreisbogens (
grüner
Pfeil in Abb. rechts) ist b
.
d
f
. Somit gilt:
d
s
= b
.
d
f
.
db
|
 |
 Wohin wird ein Teilchen gestreut, wenn seine Flugrichtung wie in rechter Abb. um
d
f
verändert wird?
Wohin wird ein Teilchen gestreut, wenn seine Flugrichtung wie in rechter Abb. um
d
f
verändert wird?
|
Wenn wir voraussetzen, dass das für die Streuung verantwortliche Potential
radialsymmetrisch
ist, also
nur vom Abstand
abhängt, ändert sich
nichts
!
|
! Das Teilchens beschreibt auch nach der Streuung eine Flugbahn, die gegenüber der unveränderten Bahn um
d
f
"verdreht" ist.
|
|
 Wohin wird ein Teilchen gestreut, dessen Flugbahn durch
d
s
geht?
Wohin wird ein Teilchen gestreut, dessen Flugbahn durch
d
s
geht?
|
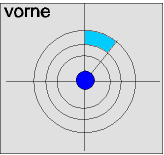
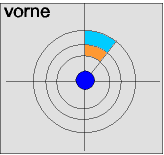
Dazu betrachten wir kurz die Abbildungen rechts. Die linke Abbildung zeigt die Ebene senkrecht zur Flugrichtung, durch die das Teilchen
vor
der Streuung fliegt. Wir nehmen an, dass das Teilchen irgendwo durch die
orange
Teilfläche fliegt. Die rechte Abbildung steht hinter dem Streuzentrum und stellt sozusagen eine
Ziel
scheibe dar. Teilchen, die
vorne
durch die
orange
Teilfläche geflogen sind, treffen im
Ziel
alle in die
rote
Teilfläche.
|
 |
 |
|
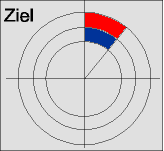
Geht nun ein Teilchen durch
d
s
(
hellblaue
Teilfläche
vorne
), so wird es
schwächer
gestreut. Es muss also im Bereich der
dunkelblauen
Teilfläche auf die Zielscheibe treffen.
|
 |
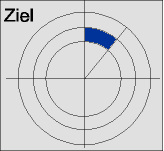 |
Im direkten Vergleich der beiden Fälle sieht man, wie sich die Streurichtung verändert, wenn ein Teilchen durch
d
s
fliegt.
Dazu sind im unteren Abbildungspaar jeweils beide Teilflächen eingezeichnet. Folgende Flächen gehören zusammen:
orange
zu
rot
und
hellblau
zu
dunkelblau
.
|
 |
 |
Statt den Abstand zweier Flugbahnen in einer bestimmten Entfernung vom Streuzentrum anzugeben, gibt man die Differenz
d
q
der beiden Streuwinkel an.
Analog dazu gibt man statt einer Teilfläche in einer bestimmten Entfernung vom Streuzentrum einen sogenannten
Raumwinkel
an.
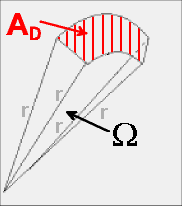
Einen
Raumwinkel
bestimmt man dadurch, dass man
alle Punkte des Randes einer Fläche
(z.B.
A
D
, siehe rechts) mit dem Mittelpunkt verbindet.
Ist
r
der Radius der Kugel, auf deren Oberfläche man die Teilfläche
A
D
|
 |
|
betrachtet, so gilt für den Raumwinkel
W
der Zusammenhang:
W
= A
D
/r
2
|
|
Für ein (infinitesimal) kleines
Raumwinkelelement
schreibt man
d
W
.
Die zentrale Aussage über die Flugbahn eines Teilchens lautet:
 Teilchen, die durch
d
s
fliegen, werden in ein Raumwinkelelement
d
W
gestreut.
Teilchen, die durch
d
s
fliegen, werden in ein Raumwinkelelement
d
W
gestreut.
|
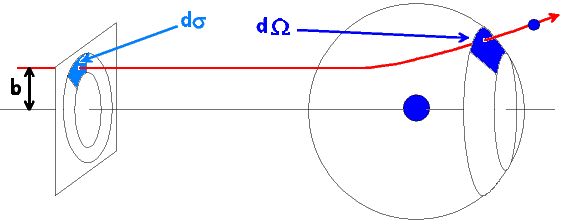
Die folgende Abbildung veranschaulicht eine entsprechende Flugbahn, man blickt dabei von der Seite auf die Bahn (
rot
).
|
|
|



