|
Angeregte
Zustände & Co. -
Erzeugung von Resonanzen
Resonanzen sind angeregte
Zustände, die im Allgemeinen nur eine extrem kurze
Lebensdauer
in der Größenordnung von
10
-23
s
haben. Oft bewegen sie sich mit einer Geschwindigkeit nahe der Lichtgeschwindigkeit. Während
ihrer Lebensdauer kommen sie daher nur einige
Femtometer
voran
(1 fm = 10
-15
m; Größenordnung
|
ihres Durchmessers). Sie hinterlassen deshalb natürlich auch keine Spuren in Blasenkammern o.ä., sondern können
nur über die
Energien und Impulse ihrer Zerfallsprodukte
identifiziert werden.
(siehe dazu auch
![zum Literaturverzeichnis; [SP3 1986, S. 169]](../button_gifs/booksm.gif) )
)
|
|
Beispiel:
Zur
Untersuchung des Aufbaus der
Nukleonen
(Protonen und Neutronen) kann man sie in einen
angeregten
Zustand (Resonanz)
versetzen und beobachten, was beim Übergang
zurück in den
Grundzustand
passiert.
Die Anregung kann dabei z.B. mit hochenergetischen Elektronen
|
oder Photonen
 geschehen. Die Anregung mit Photonen bietet gegenüber Elektronen den Vorteil, dass sie vom Nukleon vollständig absorbiert werden. Der Energieübertrag ist also, nicht wie bei unelastischen Stößen durch Elektronen
nur
teilweise, sondern gleich der
ganzen Energie
des Photons. geschehen. Die Anregung mit Photonen bietet gegenüber Elektronen den Vorteil, dass sie vom Nukleon vollständig absorbiert werden. Der Energieübertrag ist also, nicht wie bei unelastischen Stößen durch Elektronen
nur
teilweise, sondern gleich der
ganzen Energie
des Photons.
|
|
Bei ersten Experimenten beobachtete man, dass die Nukleonen bei der Rückkehr in den Grundzustand
Pionen (
p
+
)
abstrahlten. Aus den Energien der Pionen ließen sich aber nur wenige Rückschlüsse ziehen, da sie aus den Zerfällen sehr vieler
Resonanzen stammten (siehe Abb. rechts für den Prozess
g
+ p
à
n +
p
+ ).
Dabei ist wichtig, dass die Unterscheidung einzelner Resonanzen in rechter
Abbildung erst nachträglich vorgenommen wurde. Obwohl einige Resonanzen dominieren, lassen sich aufgrund der Vielzahl der "versteckten" Beiträge nur wenige Rückschlüsse ziehen. Man erkennt, dass auch wieder
die
D
13
(1520)
-Resonanz
- neben vielen anderen Resonanzen - entsteht.
|
 |
Verbessert wird die Situation, wenn man die Energie der Photonen erhöht. Neben
den Pionen werden dann auch auch
Eta-Mesonen (
h
)
produziert. Aus einer Vielzahl von Pionen werden die Eta-Mesonen herausgefiltert.
Da das
h
Isospin I =
0 hat, müssen Resonanzen, die in
h
`
s
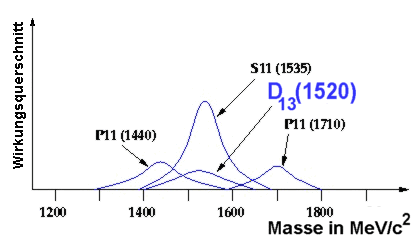
zerfallen I = 1/2 haben. Die Spektren der
h
`
s lassen sich daher leichter interpretieren, weil es durch die Einschränkung auf I = 1/2 weniger Resonanzen gibt, aus denen sie entstehen können
(siehe Abb. rechts; mögliche Resonanzen für den Prozess
g
+ p
à
p +
h
).
Auch hier ist wieder die
D
13
(1520)
-Resonanz
dabei.
|
 |
Die Experimente fanden
am Strahlplatz PHOENICS der Beschleunigeranlage ELSA in Bonn statt.
|
|
 Wie kann man aus dem Wissen über das Vorkommen verschiedener Resonanzen
etwas über die Struktur der Nukleonen herausbekommen?
Wie kann man aus dem Wissen über das Vorkommen verschiedener Resonanzen
etwas über die Struktur der Nukleonen herausbekommen?
Wir haben bei den angeregten Zuständen des Quecksilberatoms gesehen, dass das
Energieniveau eines Zustands mit seinen
Quantenzahlen
(Spin s, Isospin I etc.
 ) verbunden war.
Unterschiedliche Quantenzahlen
führen zu
unterschiedlichen Energieniveaus.
Bei Resonanzen ist dies genauso. Aus der Kenntnis der Energieniveaus (d.h.
) verbunden war.
Unterschiedliche Quantenzahlen
führen zu
unterschiedlichen Energieniveaus.
Bei Resonanzen ist dies genauso. Aus der Kenntnis der Energieniveaus (d.h.
|
der Masse) der Resonanzen kann man Rückschlüsse auf die entsprechenden
Quantenzahlen ziehen.
Aus den Quantenzahlen lassen sich wiederum Rückschlüsse auf die Eigenschaften der Nukleonen ziehen, die die Grundzustände der Resonanzen sind.
|
|
 Angeregte Zustände (z.B. Resonanzen), ihre Energieniveaus und Übergänge zwischen den Energieniveaus lassen Rückschlüsse auf gewisse Eigenschaften
der Grundzustände zu.
Proton und Neutron sind
die Grundzustände der
Angeregte Zustände (z.B. Resonanzen), ihre Energieniveaus und Übergänge zwischen den Energieniveaus lassen Rückschlüsse auf gewisse Eigenschaften
der Grundzustände zu.
Proton und Neutron sind
die Grundzustände der
|
Nukleonenresonanzen.
Die Resonanz D
13
(1520) hatte natürlich noch nicht direkt nach ihrer Entdeckung diese Bezeichnung,
denn in "
D
13
"
sind bereits Informationen über
Spin, Isospin und Bahndrehimpuls enthalten:
|
|
 Der Index "
13
"
ist dabei als "
eins-drei
" zu lesen,
denn die erste Ziffer "
1
"
gibt den
Isospin
I
der Resonanz an: I =
1
. 1/2
=
1
/2.
Der Index "
13
"
ist dabei als "
eins-drei
" zu lesen,
denn die erste Ziffer "
1
"
gibt den
Isospin
I
der Resonanz an: I =
1
. 1/2
=
1
/2.
Man beachte, dass
alle Resonanzen in der kleinen obigen Grafik den Index "
1
",
also I = 1/2 haben.
 An der zweiten Ziffer "
3
"
kann man den
Spin s
ablesen: s =
3
. 1/2
=
3
/2
An der zweiten Ziffer "
3
"
kann man den
Spin s
ablesen: s =
3
. 1/2
=
3
/2
 Das "
D
" bezeichnet den
Bahndrehimpuls
l
= 2
.
Das "
D
" bezeichnet den
Bahndrehimpuls
l
= 2
.
 Mit diesen Erklärungen versteht man nun auch die Bezeichnungen der anderen
Resonanzen (siehe große Abb. oben), z.B.
F
37
(1950)
.
Welchen Bahndrehimpuls, Spin und Isospin besitzt dieser Zustand?
Mit diesen Erklärungen versteht man nun auch die Bezeichnungen der anderen
Resonanzen (siehe große Abb. oben), z.B.
F
37
(1950)
.
Welchen Bahndrehimpuls, Spin und Isospin besitzt dieser Zustand?
|
|
|
(siehe
dazu auch
![zum Literaturverzeichnis; [LOH 1992, S. 43]](../button_gifs/booksm.gif) )
)
|