|
Grundlagen
der QM -
Die quantenmechanische Wellenfunktion
Y
(x,
t)
|
Bei der Beschreibung der Elektronenbeugung und -interferenz haben wir gesehen, dass Elektronen wellenähnliches Verhalten zeigen. Wir konnten einem Elektron eine Wellenlänge
(
de Broglie ) zuordnen, die mit seinem Impuls verknüpft ist. Grundsätzlich
gilt dies nicht nur für Elektronen, sondern
für alle Teilchen
|
des Mikrokosmos : Leptonen, Quarks, Protonen, Neutronen
usw.
Die Quantenmechanik (QM) löst die gegensätzlichen Vorstellungen "einerseits Teilchen, andererseits Welle" durch eine Wahrscheinlichkeitsinterpretation ("Bornsche Deutung") auf. Mehr dazu auf den folgenden Seiten.
|
Anmerkung:
Der Begriff "Welle-Teilchen-Dualismus" wird nicht mehr verwendet, da der scheinbare Dualismus durch die Interpretation der QM aufgelöst wird.
Vgl.
![zum Literaturverzeichnis; [BAD 1996]](../button_gifs/booksm.gif) oder oder
![zum Literaturverzeichnis; [WIE 2001]](../button_gifs/booksm.gif) |
 An Stelle vom "klassischen Teilchen" spricht man in der QM vom "quantenmechanischen
Zustand" eines Objekts, beschrieben durch eine
komplexe Wellenfunktion.
An Stelle vom "klassischen Teilchen" spricht man in der QM vom "quantenmechanischen
Zustand" eines Objekts, beschrieben durch eine
komplexe Wellenfunktion.
 Was bedeutet "
Zustand
"?
Was bedeutet "
Zustand
"?
|
Betrachten wir dazu eine Welle. Man kann für
einen festen Ort oder Zeit die Wellenlänge oder die
Elongation
einer Welle angeben. Dies kann durch Messung geschehen oder einfacher durch Rechnung, wenn man den Funktions- term, der die
Wellenausbreitung beschreibt, kennt.
|
|
Beispiel:
Betrachten wir eine ebene,
monochromatische Welle; ihre Elongation A(x, t) zum Zeitpunkt t am Ort x lautet (klassische Beschreibung!):
A(x, t) = A
0
sin(kx -
w
t)
Das ist eine sinusförmige Welle mit der Frequenz
n
=
w
/2
p
, der
Wellenzahl k, |
k = 2
p
/
l
und der Amplitude A
0
.
Am
Ort
x = 0 zum
Zeit
punkt t = 0 hat sie die
Elongation
A(0, 0) = 0. Wir können also unter Benutzung des Funktionsterms Aussagen über die
Elongation
in beliebigen
Ort
en zu beliebigen
Zeit
en machen.
|
|
Wellenfunktionen werden meist mit
Y
(griech. Buchstabe, großes "Psi") bezeichnet.
Die Funktion, die in unserem Beispiel die Elongation der monochromatischen Welle
beschreibt, ist eine - wenn auch idealisierte und reelle - Wellenfunktion.
Man spricht allgemein von der
Wellenfunktion
oder der
Amplitude
Y
.
|
 An Stelle von klassischen Teilchen, denen gleichzeitig ein bestimmter Ort und Impuls zugeordnet werden kann,
spricht man in der Quantenmechanik nur von
Zuständen von Quantenobjekten,
die durch eine
komplexe Wellen- funktion
Y
beschrieben werden
(zeitabhängig in Ortsdarstellung:
Y
(x, t)). Die Kenntnis der Wellenfunktion ist elementar wichtig, da mit ihr Vorhersagen über Quantenobjekte
gemacht werden können.
An Stelle von klassischen Teilchen, denen gleichzeitig ein bestimmter Ort und Impuls zugeordnet werden kann,
spricht man in der Quantenmechanik nur von
Zuständen von Quantenobjekten,
die durch eine
komplexe Wellen- funktion
Y
beschrieben werden
(zeitabhängig in Ortsdarstellung:
Y
(x, t)). Die Kenntnis der Wellenfunktion ist elementar wichtig, da mit ihr Vorhersagen über Quantenobjekte
gemacht werden können.
|
 |
In der Quantenmechanik wählt man zur Beschreibung von Wellen die komplexe Darstellung. Gegenüber der klassischen Wellenfunktion, die nur die Elongation angibt, hat dies den Vorteil, dass mit der komplexen Wellenfunktion Amplitude und Phasenlage zu jedem Zeitpunkt und an jedem Ort angegeben werden können. Die komplexe Wellenfunktion
lautet:
Y
(x,t) =
A
0
cos(kx-
w
t) + iA
0
sin(kx-
w
t)
Mit der Eulerformel (e
i
f
= cos
f
+ i
.
sin
f
) kann man die Wellenfunktion unseres Beispiels umformen zu:
 Y
(x,
t) = A
0
.
e
i(kx-
w
t)
Y
(x,
t) = A
0
.
e
i(kx-
w
t)
Dies ist die übliche Darstellung einer
ebenen Welle. Mit den Beziehungen
für Impuls p (k = 2
p
p/h)
und Energie E
(
w
= 2
p
E/h) kann man sie nochmals umformen: |
 Y
(x,
t) = A
0
.
e
2
p
i(px-Et)/h
Y
(x,
t) = A
0
.
e
2
p
i(px-Et)/h
Anschaulich dargestellt, beschreibt diese komplexe Funktion eine komplexe Zahl mit fester Amplitude
A
0 (in der komplexen Ebene entspricht dies dem Abstand vom Ursprung) und einem zeitabhängigen Polarwinkel
(kx -
w
t). Diese Zahl wird also durch einen Punkt im Abstand A
0 vom Ursprung repräsentiert,
der mit der Winkelgeschwindigkeit
w
um den Ursprung rotiert. Man verwendet zur Veranschaulichung daher rotierende Zeiger, die vom Ursprung zur entsprechenden komplexen Zahl zeigen. Ihre Länge entspricht der Amplitude und ihre Zeigerstellung der sogenannten Phasenlage. |
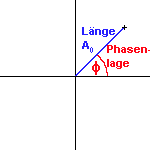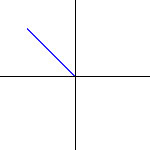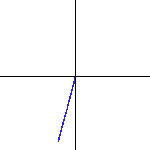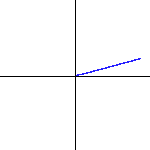
|
Den Zusammenhang zwischen klassischer Wellengleichung, die die Elongation einer Welle beschreibt, und der komplexen Darstellung, die sowohl Amplitude als auch die zugehörige Phasenlage beschreibt, zeigt folgendes JAVA-Applet. Die obere der beiden Reihen einzelner Punkte längs der Ausbreitungsrichtung der Welle zeigt die Veränderung der Elongation an jedem der Punkte. Die untere Reihe zeigt durch die
rotierenden Zeiger sowohl Elongation als auch Phasenlage an. Wellenlänge und Frequenz lassen sich im Applet variieren.

|
Man beachte, dass der Begriff
Amplitude in der Quantenmechanik
gegenüber der klassischen Physik eine erweiterte Bedeutung besitzt. Klassisch ist die
Amplitude einer Schwingung die maximale Auslenkung (maximale Elongation). In der Quantenmechanik |
wird der Wert der Wellenfunktion an einem Ort zu einer bestimmten Zeit als
Amplitude bezeichnet.
Einen weiteren Einblick in die Darstellung von Wellenfunktionen mit Phasenzeigern gibt folgende Tour:
 |
|
|


![zum Literaturverzeichnis; [BAD 1996]](../button_gifs/booksm.gif)
 Was bedeutet "
Zustand
"?
Was bedeutet "
Zustand
"?


