Feynman-Diagramme und Feynman-Kalkül - Die Kopplungskonstante in der QCD   Wir haben bei  Betrachtung der QED gesehen, dass die Beiträge von Feynman-Diagrammen mit einer großen Anzahl von Vertices vernachlässigbar werden, da die Kopplungskonstante in der QED ( a » 1/137 << 1) wesentlich kleiner als 1 ist.    Die starke Wechselwirkung macht es den Teilchenphysikern hier schwerer. Messungen der Kopplungskonstante in der QCD a s ( a s = a stark = a strong ) haben erstaunlicherweise ergeben, dass a s keine Konstante ist , sondern vom Abstand der beteiligten Quarks oder Gluonen abhängt.   Veranschaulichen wir das am Beispiel des aus Quarks zusammengesetzten Protons: Die Aussage " bei kleineren Abständen " ist gleichwertig mit der Aussage " bei höheren Energien " bzw. " bei höheren Impulsüberträgen ". Man kann sich dies ganz anschaulich so vorstellen, dass sich Teilchen umso näher kommen, je größer die Energie ist, die sie bei einem Stoß besitzen. Das Proton hat einen Durchmesser von ca. 1 fm = 10 -15 m. Betrachten wir zunächst Abstände größer als 1 fm. Hier stellt man fest, dass a s > 1 ist . Die Kopplung wird also sehr stark und das Feynman-Kalkül versagt, da immer mehr Vertices in Feynman-Diagrammen zu immer größeren Beiträgen zur Gesamtamplitude führen würden. Aufgrund dieser starken Kopplung können einzelne Quarks nicht aus Hadronen entfernt werden. Man nennt diese Erscheinung " Quark-Einschluss " oder engl. confinement " (siehe symbolisch "blaues Quark" in Abbildung rechts).    Geht man andersherum vom Protonenradius 1 fm zu immer kleineren Abständen bzw. zu höheren Impulsen Q, so nimmt a s asymptotisch gegen 0 ab, so dass die Bindung zwischen Quarks schwächer wird. Man spricht daher von " asymptotischer Freiheit " der Quarks im Inneren des Protons (siehe "grünen und roten Quark")! Wichtig ist, dass für diese kleinen Abstände, die in der Hochenergiephysik auftreten, das Feynman-Kalkül anwendbar ist! 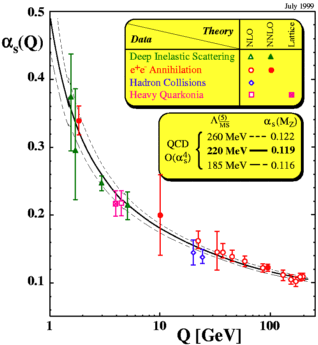(siehe dazu auch  und )  Zitat aus Wie sehr die Kopplungskonstante der starken Wechselwirkung ( a s ) vom Abstand und damit vom Impulsübertrag Q abhängt, zeigt die rechte Grafik. Dort sind eine Reihe von Messungen von a s (Q) über Q (logarithmisch!) angetragen. Man erkennt deutlich die starke Abnahme von a s. Im Vergleich zu a s nimmt die Feinstrukturkonstante a (siehe Grafik weiter unten) mit Q zu! Welche Erklärung gibt es hierfür? In den beiden folgenden kurzen Abschnitten, werden die entscheidenden Effekte bei QED und QCD verglichen. Grafik links: Kopplungskonstante der starken Wechselwirkung a s in Abhängigkeit vom Impulsübertrag Q QED: Vakuumpolarisation und Feinstrukturkonstante Virtuelle Elektron-Positron-Paare bilden eine „Wolke“ um eine elektrische Ladung herum. Hierdurch wird die Ladung im Zentrum abgeschirmt. Photonen „sehen“ daher eine kleinere, effektive elektrische Ladung. Die Kopplungskonstante ist infolgedessen für größere Abstände kleiner. Mit kleiner werdendem Abstand wird die gesehene effektive Ladung größer, der Wert der Kopplungskonstante wird größer. Kurz: Die Feinstrukturkonstante a nimmt mit kleiner werdendem Abstand bzw. entsprechend größer werdendem Impuls Q zu ! QCD: Vakuumpolarisation und Kopplungskonstante der starken Wechselwirkung Analog zur QED werden um eine starke Ladung (Farbladung) herum Quark-Antiquark-Paare gebildet. Diese schirmen die Farbladung ab. Daraus folgt wie bei der QED: Die Kopplungskonstante der starken Wechselwirkung nimmt auf Grund der virtuellen Quark-Antiquark-Paare mit größer werdendem Impuls Q zu! ABER : Dieser Effekt wird durch die Gluonen, die im Gegensatz zu den Photonen auch aneinander koppeln (Gluonschleifen; "Photonenschleifen" gibt es nicht!), überkompensiert! Auch die Gluonen bilden eine „Wolke“ um die Farbladung. Sie führt allerdings zu einer Verstärkung der Farbladung nach außen hin. Bei kleineren Abständen bzw. größer werdenden Impulsen wird die "effektive" Farbladung nun kleiner und die starke Kopplungskonstante nimmt ab. Da der verstärkende Effekt durch die Gluonen gegenüber dem abschirmenden Effekt durch die Quark-Antiquark-Paare überwiegt, nimmt die Kopplungskonstante der starken Wechselwirkung mit größer werdendem Impuls Q insgesamt ab ! Man bräuchte 16 statt 6 Quarks, um den Effekt der Gluonen zu kompensieren. 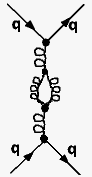Gluonschleifen der QCD Die Kopplungskonstante der starken Wechselwirkung a s ist eine sogenannte " laufende Konstante ". Nur für Abstände kleiner als ein Protonenradius (1 fm) ist sie wesentlich kleiner als 1, so dass nur dort      das Feynman-Kalkül anwendbar ist.  Die Kopplungskonstante in der QED ( a » 1/137 << 1 ist wesentlich kleiner als 1. Auch sie ist - wie oft nicht ganz korrekt dargestellt - eigentlich keine echte Konstante, sondern hängt vom Impulsübertrag Q eines Prozesses ab (" laufende " Konstante). Die rechts abgebildete Grafik mit Messdaten verdeutlicht dies. Man beachte, dass hier der Kehrwert a -1 über Q angetragen ist. Die gestrichelte Linie (konstantes a = 1/137 ) verläuft daher bei (1/137) -1 = 137 = a -1 (0). Man erkennt, dass a mit steigendem Impulsübertrag größer wird! Der durchgezogene Verlauf entspricht der Berechnung, die auf dem Standardmodell (SM) basiert ( a -1 SM (Q)). Grafik links: Kehrwert der Feinstrukturkonstanten a in Abhängigkeit vom Impulsübertrag Q Nach elektromagnetischer und starker Wechselwirkung fehlt nun noch ein Einblick in Feynman- Diagramme für Prozesse der schwachen Wechselwirkung.   Auf zur nächsten Seite!